
This article in english.
Herzlich Willkommen zur dritten Ausgabe unserer Physikserie, dieses mal live vom Urlaubsort Sissi auf Kreta (Griechenland). Das letzte mal haben wir uns mit dem wichtigsten Phänomen der Akustik beschäftigt, der Schallgeschwindigkeit. Wir haben auch gesehen, wie wir damit in einer Aufnahmesituation umgehen können.
Ich hoffe, du hast während dessen ein bisschen mit den Zahlen gespielt und dir die Formeln weitestgehend angeeignet, weil wir dieses Wissen dieses mal brauchen werden um ein paar Lautsprecher für einen Auftritt einzurichten. Doch bevor wir das tun, stimmen wir erstmal die Gitarren.
Als du auf die Bühne siehst, fallen dir sofort die ganzen Gitarren und Lautsprecher auf. Der Grund für einen Haufen Gitarren liegt ja noch auf der Hand, aber warum in aller Welt nur so viele Lautsprecher? Am Ende dieses Artikels wirst du wissen, was sich der Techniker da nur gedacht hat.
Saiteninstrumente mit den Ohren zu stimmen ist gar nicht so schwer, wie man meinen möchte. Was passiert eigentlich, wenn zwei Schallquellen gegeneinander verstimmt sind? Nehmen wir dazu den einfachsten Fall, zwei Sinustöne, an. Die folgenden Schaubilder zeigen Bildschirmfotos eines Windowsprogrammes, dass ich zur Demonstration geschrieben habe.
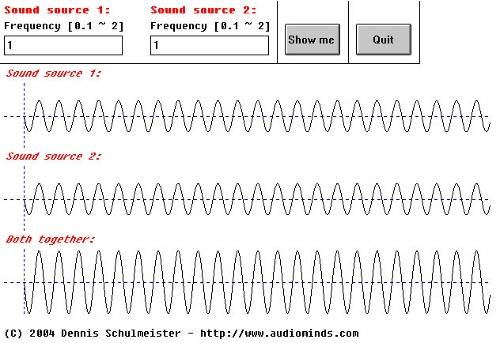
Akusitk 3.1
Diese Abbildung zeigt zwei exakt gleich gestimmte Schallquellen. Wie du weißt, ist Schall additiv, das heißt, der resultierende Klang hat die selbe Frequenz wie die beiden Schallquellen, ist aber doppelt so laut.
Was aber, wenn die Tonerzeuger verstimmt sind? Hier müssen wir zwischen verschiedenen Fällen unterscheiden:
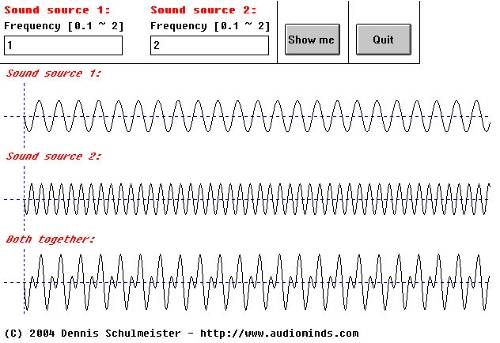
Akusitk 3.2
In diesem Fall treten so genannte Obertöne auf. Die Obertöne einer Frequenz lassen sich ganz einfach errechnen:
fo = k * f ; k e N [Hz]
k e N (sprich: k Element N) bedeutet, dass k aus der Menge der natürlichen Zahlen genommen wird. Natürliche Zahlen sind alle Zahlen größer Null ohne Nachkommastellen. Mehr gibt es nicht zu beachten, wenn du es mit Obertönen zu tun bekommst.
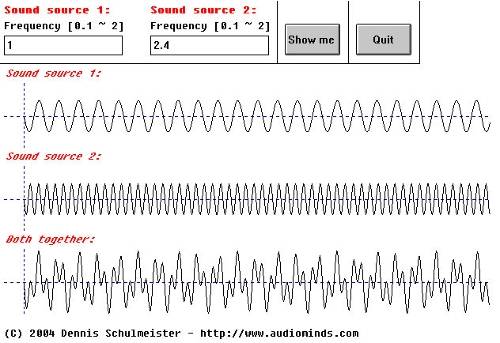
Akusitk 3.3
Das Schaubild sieht total wirr aus, ist aber nicht all zu schwer zu verstehen. Das einzige, was man hören kann sind - zwei verschiedene Töne. Aber nur solange ihre Frequenzen nicht zu nahe bei einander liegen.
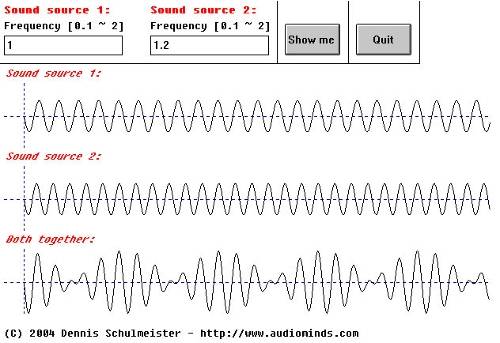
Akusitk 3.4
Bis jetzt ist das der wichtigste Fall. Der entstehende Klang wird ein wenig Chorushaft klingen (obwohl Chorus noch etwas anders funktioniert. Chorus ändert die Differenzfrequenz vor und zurück während einer gewissen Zeit). Dieser Klang wird auch oft als "Schwebung" bezeichnet.
Obwohl das Schaubild immer noch total verrückt aussieht, kann man schon ganz gut die Stellen entdecken, wo die Amplitude für eine kurze Weile nahe der Null ist. Um so was mit den Ohren zu erkennen braucht man ein wenig Übung. Hat man es allerdings oft genug gehört, fällt einem auf, dass der Klang ständig lauter und leiser wird.
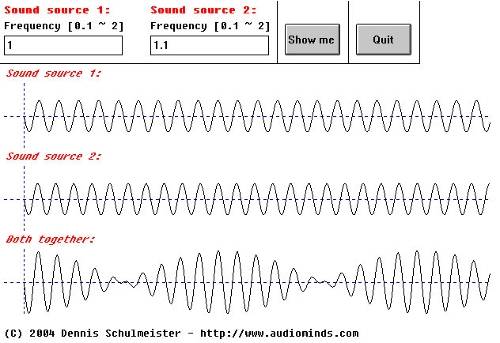
Akusitk 3.5
Dieser Fall ist sogar noch interessanter. Jetzt kann man die Nullstellen ganz leicht erkennen und auch hören. Der klang wird sanft aus und wieder ein geblendet. Je näher sich die Frequenzen annähern, desto länger dauern die Aus- und Einblendungen und desto weniger treten sie auf.
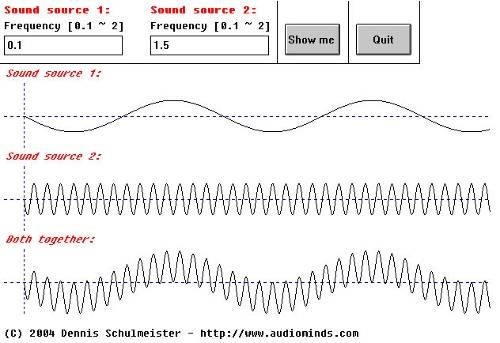
Akusitk 3.6
Ok, ich gebe zu, dass dieser Fall nicht viel damit zu tun hat, Instrumente zu stimmen, da nicht mal gute, elektronische Synthesizer tiefe Töne bis zu 5 Hz erzeugen können. Allerdings gibt das Schaubild eine ausgezeichnete Illustration. Wir sehen, dass die entstehende Welle ein perfekter Hybrid beider Erzeugerwellen ist. Es ist nahezu unmöglich, so was per Ohr zu erkennen, ein Oszilloskop gibt aber schnell Auskunft.
Mit den obigen Informationen solltest du nun gut gerüstet sein, um mit den Gitarren auf der Bühne fertig zu werden. Wenn du allerdings nicht gerade ein absolutes Gehör hast, wirst du einen zusätzlichen Referenzton benötigen, um die erste Gitarrensaite zu stimmen. Vielleicht siehst du zu den Keyboards herüber und erinnerst dich daran, wie dir mal ein jemand erzählte, dass ein 'E' auf der weißen Taste nach den beiden schwarzen gespielt wird.
Du drückst also eine dieser Tasten und probierst die beiden Instrumente so gut wie möglich auf einander abzustimmen. (Um zu üben ist es natürlich auch in Ordnung, einfach davon auszugehen, dass die erste Saite immer perfekt gestimmt ist). Während du so an den Gitarren drehst, musst du an den Audiominds.com Newsletter denken und dir fällt ein, dass eigentlich nur einer der aufgezählten Fälle von Verstimmungen relevant ist. Natürlich der, wenn sich die beiden Frequenzen immer näher kommen.
Nachdem du die erste Saite überwunden hast, ist der Rest nicht mehr so schwer. Spiele einfach die Note der zu stimmenden Saite auf der nächst tieferen und probiere sie so gut wie möglich anzugleichen. Klingen sie noch zu sehr nach einem Intervall, musst du viel drehen. Kommen sie sich aber schon recht nahe, fange an auf die "Löcher" im Klang zu hören. Je weniger davon auftauchen und je länger das Aus- und Einblenden des Klanges braucht, desto besser.
Wenn du es übertrieben hast, tauchen die "Löcher" auf einmal wieder vermehrt auf. Für die restlichen Saiten gehst du entsprechend vor. Ähnliche Techniken können übrigens auf jedes Saiteninstrument übertragen werden. (Ein Klavier zu stimmen ist dennoch eine Kunst für sich auf Grund des "Stretch Tunings". Du willst es nicht wirklich ausprobieren. --Ed)
(Ein Link zu der Software, die ich für die Schaubilder geschrieben habe, findest du am Ende dieses Artikels)
…
Ok - die Gitarren wären gestimmt. Zeit für ein Päuschen weil nun die richtige Arbeit beginnt: Die Lautsprecher müssen installiert werden. (Du solltest die Lautsprecher wirklich zuerst installieren und dann die Gitarren stimmen! --Ed.) Bevor wir uns endgültig den Rücken brechen, wäre es gescheit erst nachzudenken, wo wir die Lautsprecher überhaupt haben wollen. Einige simple, einfach zu merkende Regeln werden uns dabei helfen:
Jede akustische Quelle besitzt ein so genanntes Nahfeld und Diffusfeld (engl. Nearfield und farfield. Garfield hat natürlich nichts damit zu tun). Bei Lautsprechern lässt sich das einfach erklären:
Die meisten Boxen benutzen mehrere Lautsprecher, um verschieden Frequenzbereiche zu reproduzieren. Die einfachsten Boxen beinhalten dabei nur einen Lautsprecher oder haben einen Bass-Woofer und ein kleines Horn. 3-Weg-Systeme fügen dem noch einen Lautsprecher für die hohen Mitten hinzu.
Eine einfache Daumenregel besagt, dass die Grenze zwischen Nah- und Diffusfeld so weit vom Klangkörper wie seine größte Länge entfernt ist. Also wenn er 12 Fuß hoch, 7 Fuß lang und 9 Fuß tief ist (wie gesagt, erschienen diese Artikel zuerst im US-Raum), beginnt das Diffusfeld in 12 Fuß Entfernung von der Box. Der Unterschied beider Felder besteht darin, dass wenn sich der Zuhörer innerhalb des Nahfeldes befindet, er immer einem bestimmten Lautsprecher der Box näher als dem anderen ist. Dementsprechend ändert sich das Klangbild für ihn ständig, wenn er sich bewegt.
Im Diffusfeld hingegen ist er weit genug entfernt, so dass sich der Klang aller Komponenten genügend addiert, um keinen größeren Unterschied deutlich werden zu lassen. (Mal vom Diffusschall, der, je weiter man sich in das Diffusfeld begibt, vom Hörer noch mit aufgenommen wird und dem Diffusfeld seinen deutschen Namen verleiht.)
Bei Lautsprechern ist diese Situation so gut wie immer gegeben, will man aber ein Instrument mit Mikrofonen abnehmen, sollte man es im Hinterkopf behalten.
Herr Haas hatte einen interessanten Gedanken, der heute als das Haas-Theorem bekannt ist: Unser Gehirn ortet eine Schallquelle unter anderem an Hand der Richtung, aus der es den Schall zuerst aufnimmt. Wenn jemand zu dir von der rechten Seite spricht, hörst du ihn zwar mit beiden Ohren, aber wegen seiner weiteren Entfernung zu deinem linken Ohr, braucht es ein wenig länger, bis der Schall auch dort ankommt.
Also denkt sich dein Gehirn: "Hm, der Klang kommt zuerst am rechten Ohr an. Also muss die Schallquelle irgendwo rechts von mir sein. Rechts ist der Schall auch lauter wie links, was meine Theorie bestätigt. Äh, was hat er gerade gesagt?"
Wenn du willst, kannst du einen kleinen Test durchführen. Nimm einen Freund oder jemand aus deiner Familie und setze ihn zwischen zwei Lautsprecher. Oder setze ihm einen Kopfhörer auf. Alles was er tun muss, ist die sagen, woher der Schall kommt. Nimm dazu zwei identische Signale (wie einen gesprochenen Text) und positioniere sie ganz links und ganz rechts im Panorama. Dann mache das Linke etwas lauter, lass aber das Rechte ein paar mSek früher anfangen. Die Meisten werden wohl zuerst auf Rechts tippen.
Zurück zu unserem Auftritt und dem Stapel Lautsprecher. Es ist von essentieller Wichtigkeit, dass das Publikum den Eindruck hat, der Schall käme von der Bühne. Wir wollen aber mindestens ein Paar Lautsprecher hinten im Raum aufbauen, um der schlechten Akustik entgegen zu wirken. Hätten wir es mit einem größeren Raum zu tun, könnten wir auch noch ein Paar in der Mitte des Raumes aufbauen und so weiter.
Um es aber nicht zu kompliziert zu machen (und weil unser Raum nicht so groß ist,) installieren wir nur zwei Paar Lautsprecher. Eines vor der Bühne, eines am Ende des Raumes. Diese interessante Installation erlaubt es uns, die Lautstärke relativ niedrig zu halten und ganz nebenbei noch Probleme wie Rückkopplungen und verärgerte Zuhörer sanft zu umschiffen.
Aber wir sind noch nicht fertig. Für die Zuhörer in der vorderen Hälfte des Raumes ist alles paletti, weil sie näher der Bühne als dem Raumende sind. Aber die anderen Zuhörer hören den Schall vom Raumende vor dem Bühnenschall. Es ist immer ein bisschen peinlich, wenn der Schlagzeuger das Solo seines Lebens startet und sich das halbe Publikum nach hinten umdreht.
Also müssen wir diese Laufzeitunterschiede wieder aus bügeln. Sogar der am meisten von der Bühne entfernte Zuhörer muss die Musik erst von der Bühne hören können, dann von den Zusatzlautsprechern. Was wir tun müssen ist einfach. Letzten Monat haben wir gelernt, wie man die Zeit berechnet, die der Schall benötigt, um eine gegebene Strecke zurückzulegen.
Heute werden wir diese Formeln anwenden, um zu berechnen, wie lange es braucht, bis die Musik der Bühne am anderen Ende des Raumes gehört werden kann. Zur Erinnerung hier nochmal die Formeln:
V 0 331,4 + 0,6T [m/Sek] mit T gleich der Raumtemperatur in °C und
t = d / v (Zeit gleich Entfernung mal Geschwindigkeit)
Da die meisten Amerikaner mit Zoll, Fuß und Fahrenheit vertrauter sind hier die entsprechenden Formeln:
Zoll -> cm: CM = IN / 2,54… [cm]
cm -> Zoll: IN = CM * 2,54… [in]
Fuß -> Meter: M = FT + 0,3048… [m]
Meter -> Fuß: FT = M / 0,3048… [ft]
Wenn du es sehr genau nimmst und die entsprechende Zeit mitbringst, kannst du mit diesen Formeln sehr präzise Berechnungen anstellen. Sei dir aber Bewusst, dass es unter Anwendung der amerikanischen Maßeinheiten zu Rundungsfehlern kommen wird.
Ich hoffe, du hast noch dieses kleine Zettelchen an deinem Mischpult kleben, auf dem steht:
346,4 m/Sek = 1136,48 ft/Sek
Das ist die Durchschnittsgeschwindigkeit von Schall in Räumen, in denen die Temperatur nach menschlichem Komfort geregelt ist. Für unsere Zwecke brauchen wir nur diese Zahlen und die altbekannte Formel
t = d / v
Sagen wir. der Raum ist 10 Fuß lang (ja, ja die Amerikaner). Dann würden wir rechnen:
t = 10 / 1136,48 = 0,008799… Sek = 8 mSek
Nach spätestens 8 mSek kann also jeder im Raum die Musik hören. Auf Grund des Haas-Effekts müssen wir den Hecklautsprechern also eine Verzögerung von 8 mSek zuführen. 8 mSek wäre aber keine geeignete Verzögerungszeit, da sie bedeuten würde, dass die Zuhörer im Extremfall den Klang von beiden Richtungen gleichzeitig hören würden.
Wir wollen aber, dass man die Bühne zuerst hört. Von daher runden wir die 8 mSek eben großzügig auf 10 oder 12 mSek auf und alles ist in Ordnung. Man sollte allerdings noch bedenken, dass ich in diesem Beispiel ein zu einfaches Bild gezeichnet habe. Im wirklichen Leben kommt es nicht selten vor, dass sich die Lautsprecher irgendwo oberhalb der Ohren der Zuhörer befinden.
In diesem Falle könnte man mit dem Satz des Pythagoras die Hypotenuse eines rechtwinkligen Dreiecks (a² = b² + c² für a als Hypotenuse und b,c als Katheten). Dieses Ergebnis könnten wir wiederum in die t = d / v Formel einsetzen. Aber nicht so schnell, wenn es nicht wirklich absolut notwendig ist, wird es wohl kaum den Aufwand wert sein. "Runden" wir halt noch ein paar mSek dazu, bis es annehmbar klingt. Höre immer auf die Feinheiten, denn schließlich sind es unsere Ohren, auf die wir uns verlassen sollten, nicht die Zahlen.
Keine echten Gitarren oder Lautsprecher wurden verletzt um diesen Artikel zu schreiben. Das Wellenformprogramm gibt es hier. Diese Anwendung ist © 2004 Dennis Schulmeister / www.audiominds.com und frei Verteilbar.
Euer,
Dennis